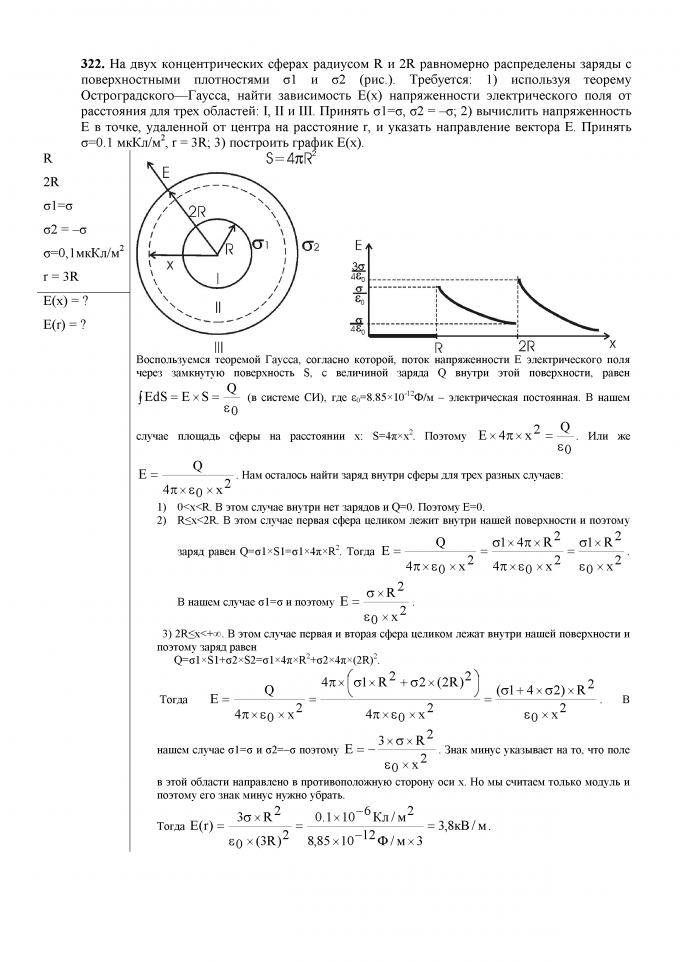
На двух концентрических сферах радиусом \(R\) и \(2R\) равномерно распределены заряды с поверхностными плотностями \({\sigma _1}\) и \({\sigma _2}\). Требуется: 1) используя теорему Остроградского—Гаусса, найти зависимость \(E(x)\) напряженности электрического поля от расстояния для трех областей: I, II и III. Принять \({\sigma _1} = \sigma \), \({\sigma _2} = - \sigma \); 2) вычислить напряженность \(E\) в точке, удаленной от центра на расстояние \(r\), и указать направление вектора \(E\). Принять \(\sigma = 0,1\) мкКл/м2, \(r = 3R\); 3) построить график \(E(x)\).
Раздел:
- Электростатика